- Polynomial interpolation (this article)
- Technique of orthogonal collocation for the solution of ordinary differential equations
- Orthogonal collocation for the solution of partial differential equations
- Piecewise polynomial interpolation focusing on quadratic and cubic splines
- Orthogonal collocation on finite elements for the solution of ordinary differential equations
- Orthogonal collocation on finite elements for the solution of partial differential equations
I will largely be using MATLAB for this series though I'll make an effort to also provide the equivalent Python code.
So let's start with idea of polynomial interpolation. Consider the case where we have $N + 1$ points and we wish to generate an $N$th order polynomial that passes through all points.
These $N+1$ points are referred to as knots, breaks, or collocation points in the literature. Let's denote the X-coordinate of each point by $x_i = x_1, x_2, \cdots, x_N, x_{N+1}$, and the corresponding Y-coordinate by $y_i = y_1, y_2, \cdots, y_N, y_{N+1}$.
An $N$th order polynomial has the forms,
\begin{equation}
P(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + \cdots + \alpha_{N-1} x^{N-1} + \alpha_N x^N.
\label{polynomial}
\end{equation}
Our task is to find the coefficients, $\alpha_i$ such that the polynomial passes through all our points.
Since we know the polynomial passes through all of out points $(x_i, y_i)$ we can write out an equations for each of the $N+1$ points. Specifically,
\begin{align*}
y_1 = & \alpha_0 + \alpha_1 x_1 + \alpha_2 x_1^2 + \alpha_3 x_1^3 + \cdots + \alpha_{N-1} x_1^{N-1} + \alpha_N x_1^N \\
y_2 =& \alpha_0 + \alpha_1 x_2 + \alpha_2 x_2^2 + \alpha_3 x_2^3 + \cdots + \alpha_{N-1} x_2^{N-1} + \alpha_N x_2^N \\
y_3 =& \alpha_0 + \alpha_1 x_3 + \alpha_2 x_3^2 + \alpha_3 x_3^3 + \cdots + \alpha_{N-1} x_3^{N-1} + \alpha_N x_3^N \\
\vdots & \\
y_N =& \alpha_0 + \alpha_1 x_N + \alpha_2 x_N^2 + \alpha_3 x_N^3 + \cdots + \alpha_{N-1} x_N^{N-1} + \alpha_N x_N^N \\
y_{N+1} =& \alpha_0 + \alpha_1 x_{N+1} + \alpha_2 x_{N+1}^2 + \alpha_3
x_{N+1}^3 + \cdots + \alpha_{N-1} x_{N+1}^{N-1} + \alpha_N x_{N+1}^N.
\end{align*}
So let's start with idea of polynomial interpolation. Consider the case where we have $N + 1$ points and we wish to generate an $N$th order polynomial that passes through all points.
These $N+1$ points are referred to as knots, breaks, or collocation points in the literature. Let's denote the X-coordinate of each point by $x_i = x_1, x_2, \cdots, x_N, x_{N+1}$, and the corresponding Y-coordinate by $y_i = y_1, y_2, \cdots, y_N, y_{N+1}$.
An $N$th order polynomial has the forms,
\begin{equation}
P(x) = \alpha_0 + \alpha_1 x + \alpha_2 x^2 + \alpha_3 x^3 + \cdots + \alpha_{N-1} x^{N-1} + \alpha_N x^N.
\label{polynomial}
\end{equation}
Our task is to find the coefficients, $\alpha_i$ such that the polynomial passes through all our points.
Since we know the polynomial passes through all of out points $(x_i, y_i)$ we can write out an equations for each of the $N+1$ points. Specifically,
\begin{align*}
y_1 = & \alpha_0 + \alpha_1 x_1 + \alpha_2 x_1^2 + \alpha_3 x_1^3 + \cdots + \alpha_{N-1} x_1^{N-1} + \alpha_N x_1^N \\
y_2 =& \alpha_0 + \alpha_1 x_2 + \alpha_2 x_2^2 + \alpha_3 x_2^3 + \cdots + \alpha_{N-1} x_2^{N-1} + \alpha_N x_2^N \\
y_3 =& \alpha_0 + \alpha_1 x_3 + \alpha_2 x_3^2 + \alpha_3 x_3^3 + \cdots + \alpha_{N-1} x_3^{N-1} + \alpha_N x_3^N \\
\vdots & \\
y_N =& \alpha_0 + \alpha_1 x_N + \alpha_2 x_N^2 + \alpha_3 x_N^3 + \cdots + \alpha_{N-1} x_N^{N-1} + \alpha_N x_N^N \\
y_{N+1} =& \alpha_0 + \alpha_1 x_{N+1} + \alpha_2 x_{N+1}^2 + \alpha_3
x_{N+1}^3 + \cdots + \alpha_{N-1} x_{N+1}^{N-1} + \alpha_N x_{N+1}^N.
\end{align*}
Notice that this is a linear system of equations (in terms of the unknown values of $\alpha_i$) and can be written in matrix form as,
\begin{equation} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_N \\ y_{N+1} \\ \end{pmatrix} = \begin{pmatrix} x_1^0 & x_1^1 & x_1^2 & x_1^3 & \cdots & x_1^N \\ x_2^0 & x_2^1 & x_2^2 & x_2^3 & \cdots & x_2^N \\ x_3^0 & x_3^1 & x_3^2 & x_3^3 & \cdots & x_3^N \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ x_N^0 & x_N^1 & x_N^2 & x_N^3 & \cdots & x_N^N \\ x_{N+1}^0 & x_{N+1}^1 & x_{N+1}^2 & x_{N+1}^3 & \cdots & x_{N+1}^N \\ \end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_{N-1} \\ \alpha_N \\ \end{pmatrix}. \label{eq:matrix}\end{equation}
\begin{equation} \begin{pmatrix} y_1 \\ y_2 \\ y_3 \\ \vdots \\ y_N \\ y_{N+1} \\ \end{pmatrix} = \begin{pmatrix} x_1^0 & x_1^1 & x_1^2 & x_1^3 & \cdots & x_1^N \\ x_2^0 & x_2^1 & x_2^2 & x_2^3 & \cdots & x_2^N \\ x_3^0 & x_3^1 & x_3^2 & x_3^3 & \cdots & x_3^N \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ x_N^0 & x_N^1 & x_N^2 & x_N^3 & \cdots & x_N^N \\ x_{N+1}^0 & x_{N+1}^1 & x_{N+1}^2 & x_{N+1}^3 & \cdots & x_{N+1}^N \\ \end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \vdots \\ \alpha_{N-1} \\ \alpha_N \\ \end{pmatrix}. \label{eq:matrix}\end{equation}
Let's introduce a bit of notation that will be helpful in subsequent articles. We'll denote the column vector of Y-values as $\vec{Y}$, the column vector of unknown values of $\alpha_i$ as $\vec{\alpha}$ and the matrix as $\bf{X}$.
Using this notation, our problem can be written as,
\begin{equation}\vec{Y} = \bf{X}\vec{\alpha}\label{eq:poly_matrix}\end{equation}
So
\begin{equation}\vec{\alpha} = \bf{X}^{-1}\vec{Y}\label{eq:polynomial_inverse}\end{equation}
Our problem of finding the coefficient vector boils down to simply finding the inverse of the matrix $\bf{X}$. Let's work out a problem.
I've chosen a bunch of X values, in this case the integers from one to six, and six corresponding Y-values at random from between zero and ten. Those happened to be 9.6703, 5.4723, 9.7268, 7.1482, 6.9773, and 2.1609. These six points are plotted below in Fig 2.
Plugging in our X- and Y-values into Eq. \ref{eq:matrix} gives,
\begin{equation} \begin{pmatrix} 9.6703 \\ 5.4723 \\ 9.7268 \\ 7.1482 \\ 6.9773 \\ 2.1609 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 & 16 & 32 \\ 1 & 3 & 9 & 27 & 81 & 243 \\ 1 & 4 & 16 & 64 & 256 & 1024 \\ 1 & 5 & 25 & 125 & 625 & 3125 \\ 1 & 6 & 36 & 216 & 1296 & 7776 \end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \alpha_3 \\ \alpha_4 \\ \alpha_5 \end{pmatrix}\label{eq:numerical_matrix}\end{equation}
I've chosen a bunch of X values, in this case the integers from one to six, and six corresponding Y-values at random from between zero and ten. Those happened to be 9.6703, 5.4723, 9.7268, 7.1482, 6.9773, and 2.1609. These six points are plotted below in Fig 2.
 |
| Figure 2: Six points whose Y-values are randomly generated. We wish to use Eqs. \ref{eq:poly_matrix} and \ref{eq:polynomial_inverse} to calculate the coefficients of our interpolating polynomial. |
Plugging in our X- and Y-values into Eq. \ref{eq:matrix} gives,
\begin{equation} \begin{pmatrix} 9.6703 \\ 5.4723 \\ 9.7268 \\ 7.1482 \\ 6.9773 \\ 2.1609 \end{pmatrix} = \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 \\ 1 & 2 & 4 & 8 & 16 & 32 \\ 1 & 3 & 9 & 27 & 81 & 243 \\ 1 & 4 & 16 & 64 & 256 & 1024 \\ 1 & 5 & 25 & 125 & 625 & 3125 \\ 1 & 6 & 36 & 216 & 1296 & 7776 \end{pmatrix} \begin{pmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \alpha_3 \\ \alpha_4 \\ \alpha_5 \end{pmatrix}\label{eq:numerical_matrix}\end{equation}
We can invert the matrix in Eq. \ref{eq:numerical_matrix} numerically in either MATLAB or numpy and calculate our coefficients from Eq. \ref{eq:polynomial_inverse}. The MATLAB code that generate the points, fills in the matrix values, and calculates the inverse and coefficients is given below. The code also plots the result. The plot is shown in Fig. 3.
clear all; clc; close all; % Set random seed to a constant value for reproduceablility. rng(4); % Our X values will just be evenly spaced points. % The Y values will be randomly chosen numbers between zero and ten. x = [1; 2; 3; 4; 5; 6]; y = 10 * rand(length(x),1); % Plot these points plot(x, y, 'o', 'markerfacecolor', [0 0 0]); xlim( [0, 7] ); ylim( [0, 12] ); % Define our square matrix X = [ x.^0, x.^1, x.^2, x.^3, x.^4 x.^5]; % Solve for unknown coefficients alpha = inv(X) * y; % The way I wrote the code the values of alpha go from lower to higher % powers of X as we go down the vector. MATLAB's polyval function assumes % the direction is reversed so we'll flip the alpha vector as to use % MATLAB's built-in functionaility alpha = flipud(alpha); % Plot the polynomial z = linspace(1, 6); hold on; plot(z, polyval(alpha, z), 'k'); hold off; grid on; xlabel('x'); ylabel('y'); set(gca, 'FontSize', 14);
 |
| Figure 3: Points connected by interpolating polynomial |
If you don't have access to MATLAB, below is the equivalent calulcation using Python.
import numpy as np import matplotlib.pyplot as plt # Set random seed to a constant value for reproduceablility. np.random.seed(4) # Our X values will just be evenly spaced points. # The Y values will be randomly chosen numbers between zero and ten. x = np.array( [1, 2, 3, 4, 5, 6] ) y = 10.0 * np.random.rand( x.shape[0], ); plt.plot(x, y, 'ko', markerfacecolor = 'k') plt.xlim( [0, 7] ) plt.ylim( [0, 12] ) plt.grid(True) plt.xlabel('x') plt.ylabel('y') X = np.column_stack(( x**0, x**1, x**2, x**3, x**4, x**5 ) ) alpha = np.linalg.solve(X, y) alpha = np.fliplr( [alpha] )[0] z = np.linspace(1, 6); plt.plot(z, np.polyval(alpha, z), 'k'); plt.show()
Of course, in this example, the size of the matrices are pre-determined so I constructed them by hand. Obviously, that could be done programmatically if variable numbers of points are needed.
There are a couple of issues which limit this technique as a general-purpose interpolation method. Problems arise when we have a large number of points. The solid curve in Fig. 3 doesn't seem to be an unreasonable representation of our data. In Fig. 4, we repeat the calculation for eight points whose Y-values are also chosen to be between zero and ten. As we can see, there is a large "bump" between the first and second points where the interpolating polynomial gets above 20. This wiggling phenomenon will become more and more pronounced as we increase the number of points.
 |
| Figure 4: Interpolating polynomial for six points whose Y-values are chosen randomly n the interval [0, 10] |
In Fig. 5, we take that a step further and look at fifteen points. Obviously, the resulting polynomial is a very poor representation of our data, and MATLAB throws a warning shown in Fig. 6 regarding the condition number of the matrix $\bf{X}$. As the message says, the matrix is close to singular, meaning its determinate is very close to zero. In practical terms, this means small uncertainties (due to numerical rounding) in our calculated values will have a huge effect on the shape of the resulting polynomial. In Fig. 5., this problem isn't bad enough to cause the interpolating curve to miss our points, but the wiggle effect makes this unusable for interpolation unless we confine ourselves to the middle points away from the two spikes.
 |
| Figure 5: Interpolating polynomial for 15 points. |
 |
| Figure 6: Warning message given when calculating coefficients for the 15-point interpolation |
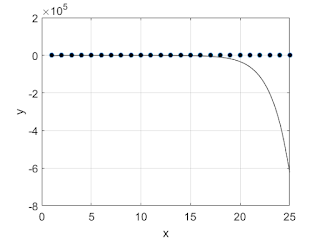
In Fig. 7, we try this technique on a large number of points and find the results fail entirely.
We will address these issues later in an article on splines, but for the next few posts, I want to show how we can use these simple interpolating polynomials to numerically solve differential and partial differential equations.
Update 11/25/2018: I've been meaning to note that the method presented here is for pedagogical purposes and is not the way I'd actually perform this operation. In practice, this is computationally inefficient, the method of Lagrange interpolating polynomials being preferable.