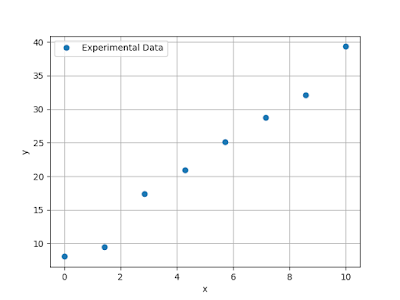
Let's assume we have taken some data and wish to model it with a straight line. Fig. 1 contains eight data points that lie long a line. I added a random number to each point just to make things a little more realistic A common way to do this is to vary the parameters that go into the model in such a way as to minimize the sum of the squared error between the model prediction and the data points, a so-called least-squares analysis.
 |
| Figure 1 |
In mathematical terms we need to find,
$$\min \sum_i \left(\mbox{f}(x_i, p) - y_i\right)^2,$$
where $p$ are our parameters and $x_i$ and $y_i$ are the x and y-values of each of our data points. In the case of simple linear problems, every spreadsheet program I know of will do this for you, and most programming languages have libraries that will do the same.
In Python (using Scipy) the code to do this is straightforward using canned linear regression routines. We don't even need consider the above equation unless we want to get under the hood and mess around or do other forms of customization. This is also simple to do in a software package like Excel, which contains basic curve-fitting tools. We will limit ourselves to Python here.
import numpy as np from scipy import stats # Set a constant random seed so the random numbers selected will always be # the same np.random.seed(2) # Set number of points num_points = 8 # Generate the points that will serve as our experimental data x = np.linspace(0, 10, num_points) y = 3 * x + 5; random_number = 7 * np.random.random(num_points) y = y + random_number # Do the regression slope, intercept, r, p, std_err = stats.linregress(x, y) # Print out the values of the slope, intercept, and correlation # coefficient. print('Slope = '+ str(slope)) print('Intercept = ' + str(intercept)) print('r = ' + str(r))
This code will print out:
Slope = 3.08771040246238
Intercept = 7.205285187141509
r = 0.9929123805249126
The built-in function also returns some statistics about the fit including the correlation coefficient between the experimental Y-values and those predicted by the model. Plotting that slope and intercept on top of our experimental data gives:
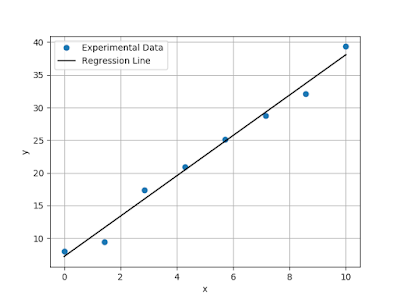 |
| Figure 2: Data points along with fit results |
This problem is very simple, and, being linear, can be worked out by hand. For the sake of argument, let's assume we couldn't do that, and furthermore, that there weren't already canned routines to do a linear regression. How might we approach this problem in that case?
One answer would be to use an optimization routine and minimize the sum of the squared errors ourselves. We can use the Python package ascipy.optimize.minimize to do this. In this case we do need to calculate calculate the least-squares error as it is the function we are actively trying to minimize.
import numpy as np from scipy.optimize import minimize # This model we are using. In this case a straight line def equation(x, m, b): return m * x + b # This is the function we actually want to minimize def objective(p, x_data, y_data): m = p[0] b = p[1] model_values = equation(x_data, m, b) res = np.sum( np.square( y_data - model_values ) ) return res # Set a constant random seed so the random numbers selected will always be # the same np.random.seed(2) # Set number of points num_points = 8 # Generate the points that will serve as our experimental data x = np.linspace(0, 10, num_points) y = 3 * x + 5; random_number = 7 * np.random.random(num_points) y = y + random_number # Initial guess of the slope and intercept p = [0., 0.] # Run the minimization routine and extract the results results = minimize(objective, p, args=(x, y)) slope = results.x[0] intercept = results.x[1] # We need to manually calculate the correlation y_model = equation(x, slope, intercept) r = np.corrcoef(y, y_model) # Print out the values of the slope, intercept, and correlation # coefficient. print('Slope = '+ str(slope)) print('Intercept = ' + str(intercept)) print('r = ' + str(r[0][1]))
This code gives the same results to with $10^{-8}$.
OK. That's an overly simple problem and is linear in nature, too. Let's look at something more complicated.
Back in the day, I did measurements of the thermodynamic properties of confined liquid helium (pure $^4$He) and mixtures of the two helium isotopes $^3$He and $^4$He as it went through the superfluid transition. We are going to concentrate on one of the mixtures here.
As part of the analysis, we need to compare our results on the confined system to that of bulk helium. That bulk specific heat at constant pressure and molar concentration of $^3$He denoted by $C_{px}$ can be calculated by interpolating previously done work. The difficulty lies in the fact that the analysis needs the specific heat at constant pressure and chemical potential difference between $^3$He and $^4$He. This quantity is denoted by $C_{p\phi}$. The calculation of this transformation invokes derivatives of various thermodynamic quantities at $T_\lambda$. Again, a lot of this has been measured historically and we'll just state that we can simply transform from $C_{px}$ to $C_{p\phi}$ easily.
The difficult part is that we also need to transform the reduced temperature $t$, which is the distance from the $\lambda$-line along a path of constant temperature, to a difference reduced temperature $\theta$, the distance to the $\lambda$-line along a path of constant chemical potential difference. The expression "$\lambda$-line" denotes that the phase transition temperature, $T_\lambda$, changes as a function concentration. Thus if we vary the concentration $x$, we'd could plot a locus of phase transitions as a function of $x$ and $T$. This curve is where the superfluid transition occurs and where we need to evaluate certain thermodynamic derivatives in our analysis, hence the repeated reference to $\lambda$-line derivatives.
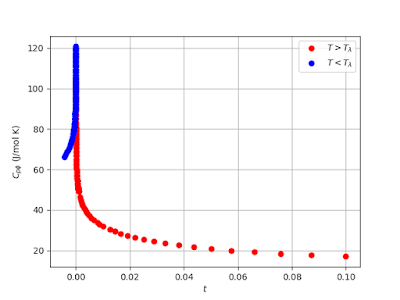
Fig 3. summarizes what he have. It shows the specific heat of a mixture as it goes through the superfluid transition at the temperature $T_\lambda$ However, the data below is plotted as a function of reduced temperature, $t = (T - T_\lambda) / T_\lambda$ where we want it to be a function of $\theta$
The relation between $C_{p\phi}$ and $\theta$ is given by,
\begin{equation} C_{p\phi} = \frac{A}{\alpha}\theta^{-\alpha}(1+D\theta^\Delta)+B.\label{eq:specific_heat} \end{equation}
Here, the parameters to be determined are $A$, $\alpha$, $D$, and $B$. $\Delta$ has a value of 0.5. The value of $A$, the amplitude of the specific heat is different on either side of $T_\lambda$ as is the value of $B$. I will use $A^\prime$ to denote the amplitude below $T_\lambda$ and $A$ above. Likewise, $B^\prime$ is for $T < T_\lambda$ and $B$ is for temperatures above the superfluid transition.
The process of converting $t$ to $\theta$ is is as follows:
First we code up Eq. 1.
Next, we code up our least-squares function that will actually be minimized. This function takes out parameter vector $q$ as well as additional arguments for reduced temperatures on either side of the transition, and the known bulk specific heats, also on both sides of the transition.
OK. That's an overly simple problem and is linear in nature, too. Let's look at something more complicated.
Back in the day, I did measurements of the thermodynamic properties of confined liquid helium (pure $^4$He) and mixtures of the two helium isotopes $^3$He and $^4$He as it went through the superfluid transition. We are going to concentrate on one of the mixtures here.
As part of the analysis, we need to compare our results on the confined system to that of bulk helium. That bulk specific heat at constant pressure and molar concentration of $^3$He denoted by $C_{px}$ can be calculated by interpolating previously done work. The difficulty lies in the fact that the analysis needs the specific heat at constant pressure and chemical potential difference between $^3$He and $^4$He. This quantity is denoted by $C_{p\phi}$. The calculation of this transformation invokes derivatives of various thermodynamic quantities at $T_\lambda$. Again, a lot of this has been measured historically and we'll just state that we can simply transform from $C_{px}$ to $C_{p\phi}$ easily.
The difficult part is that we also need to transform the reduced temperature $t$, which is the distance from the $\lambda$-line along a path of constant temperature, to a difference reduced temperature $\theta$, the distance to the $\lambda$-line along a path of constant chemical potential difference. The expression "$\lambda$-line" denotes that the phase transition temperature, $T_\lambda$, changes as a function concentration. Thus if we vary the concentration $x$, we'd could plot a locus of phase transitions as a function of $x$ and $T$. This curve is where the superfluid transition occurs and where we need to evaluate certain thermodynamic derivatives in our analysis, hence the repeated reference to $\lambda$-line derivatives.
Fig 3. summarizes what he have. It shows the specific heat of a mixture as it goes through the superfluid transition at the temperature $T_\lambda$ However, the data below is plotted as a function of reduced temperature, $t = (T - T_\lambda) / T_\lambda$ where we want it to be a function of $\theta$
The relation between $C_{p\phi}$ and $\theta$ is given by,
\begin{equation} C_{p\phi} = \frac{A}{\alpha}\theta^{-\alpha}(1+D\theta^\Delta)+B.\label{eq:specific_heat} \end{equation}
Here, the parameters to be determined are $A$, $\alpha$, $D$, and $B$. $\Delta$ has a value of 0.5. The value of $A$, the amplitude of the specific heat is different on either side of $T_\lambda$ as is the value of $B$. I will use $A^\prime$ to denote the amplitude below $T_\lambda$ and $A$ above. Likewise, $B^\prime$ is for $T < T_\lambda$ and $B$ is for temperatures above the superfluid transition.
The process of converting $t$ to $\theta$ is is as follows:
- Initially assume $t = \theta$.
- Fit Eq. \ref{eq:specific_heat}.
- Use parameters to convert $t$ to $\theta$.
- Iterate steps 2 and 3 until the ratio $A/A^\prime$ converges.
First we code up Eq. 1.
# This is Eq. 1 def equation(p, theta): # Extract individual parameters from p vector A = p[0] alpha = p[1] B = p[2] D = p[3] # Return specific heat return (A/alpha) * np.power(theta, -alpha) * (1.0 + D * np.power(theta, 0.5)) + B
Next, we code up our least-squares function that will actually be minimized. This function takes out parameter vector $q$ as well as additional arguments for reduced temperatures on either side of the transition, and the known bulk specific heats, also on both sides of the transition.
def objective(q, theta_warm, theta_cold, C_warm_exp, C_cold_exp): # Extract the parameters from the array q and calculate the specific # heat on the warm side # Format is (A, APrime, alpha, B, D, Dprime) p = [q[0], q[2], q[3], q[4]] C_warm = equation(p, theta_warm) # Extract the parameters from the array q and calculate the specific # heat on the cold side p = [q[1], q[2], q[3], q[5]] C_cold = equation(p, theta_cold)
error_warm_sq = np.square(C_warm - C_warm_exp) error_cold_sq = np.square(C_cold - C_cold_exp) res = np.sum(error_warm_sq) + np.sum(error_cold_sq) return res
Next, we set up some variables specifically for this concentration.
conc = 0.1485 # mixture 1 Tlambda = 1.963165835 # mixture 1 # Calculate lambda-line derivatives dX_dT = calc_dX_dT(conc) dphi_dT = calc_dphi_dT(conc) dS_dT = calc_dS_dT(conc) # Take theta = t initially theta_warm = t_warm theta_cold = t_cold
Lastly, we fit and iterate.
# Initial guess for our parameters q = [7.0, 10.0, -0.021, 375.0, -0.01, -0.01] for i in range(5): results = minimize(objective, q, args=(theta_warm, theta_cold, bulk_warm, bulk_cold), method='Powell' ) # Format is (A, APrime, alpha, B, D, Dprime) A = results.x[0] Aprime = results.x[1] alpha = results.x[2] B = results.x[3] D = results.x[4] Dprime = results.x[5] print A/Aprime print 'Iteration', i+1, results.success # T-to-thea calculation theta_warm = t_warm * ( 1. - dX_dT**(-1.) * dphi_dT**(-1.) * ( dS_dT -(1./Tlambda)*(A/alpha*theta_warm**(-alpha)* (1./(1.-alpha) + D*theta_warm**0.5 /(0.5 - alpha + 1) ) + B)))**(-1) theta_cold = t_cold * ( 1. - dX_dT**(-1.) * dphi_dT**(-1.) * ( dS_dT -(1./Tlambda)*(Aprime/alpha*theta_cold**(-alpha)*( 1./(1.-alpha) + Dprime*theta_cold**0.5 /(0.5 - alpha + 1.) ) + B)))**(-1.) # Use newly fitted parameters as our new initial guesses q = results.x
The number of iterations is hard coded in the example above. In practice, one would likely look at the ratio $A/A^\prime$ each iteration and seem how much it changes. If the change falls below some tolerance, one would stop the process.
 |
| Figure 4: Bulk specific heat plotted along with the fit results. |
This example is simple enough where we could probably get away with the curve_fit function included in scipy.optimize.
The code will return the following results:
$A = 9.334426752192908$
$A^\prime = 8.69867448279229$
$\alpha = -0.02185117731336304$
$B = 412.4595717146204$
$D = -0.07295632878279142$
$D^\prime = -0.3560880053296793$
Plugging these numbers back into our model and plotting the results on our data is shown in Fig 4. But perhaps a clearer way in this case to see the results is to plot these on a semilog plot. Since the specific heat follows a near power law, the semilog plot shroud be almost linear. This is shown below in Fig 5. Note, we use the absolute value of $\theta$ for $T < T_\lambda$ because of the issue in taking logs of negative numbers.
 |
| Figure 5: A plot of the specific heat and fit on a semilog scale for clarity. The absolute value of $\theta$ is plotted on the X-axis as to avoid issues with taking the log of a negative number. |
In solving this problem, there are a couple of issues I didn't address. There is a possibility of local minima. This is actually the biggest issue with what I've done above and one which I ignored entirely.
The other issue is that the parameters vary over several orders of magnitude. The biggest parameter, $B$, turns out to be on the order of $10^2$, and the smallest, $\alpha$, is on the order of $10^{-2}$. So there are about four orders of magnitude between those parameters. One can often get convergence issues if the parameters differ in size over a vast range. We can get away with it here, but in a lot of problems I work on, the parameters can vary over 19 orders of magnitude. One potential way to deal with this is to fit to the log of the parameters rather than the parameters themselves. This will tend to put them all on an even footing. For example of one parameter is on the order of $10^{-15}$ and the other of order $10^4$, $\log(10^{-15}) = -15$ and $\log(10^4) = 4$. These numbers are much easier to work with in terms of getting convergence.
The last issue is the potential for certain parameter values used by the code in the optimization to return a value of $\pm\infty$ for either the model or its gradient. I neglected to say anything about this previously, but it is why I set the method equal to 'Powell' in the minimization function. This is a gradient-free method which allows for a work-around in this case.
Neither of the above examples is particularly difficult, but the helium example has different equations on either side of the transition with some parameters shared between both sides while other parameters differ. I wanted to sketch out a general approach on how to set up and solve these sorts of problems.